Yo~ Konnichiwa sobat Otatechnime
Kali ini, mimin akan berikan pengertian dari Proposisi yang ada pada logika Matematika.
Apa sih Proposisi itu?
Jadi, Proposisi merupakan suatu statement atau pernyataan pada matematika dimana statement tersebut digunakan sebagai kalimat dalam penalaran yang memiliki nilai Benar (True) atau bernilai Salah (False).
Statement pada proposisi yang ada pada matematika biasanya mengandung simbol p, q, dan r. Simbol-simbol itu merupakan simbol umum untuk identitas kalimat pada proposisi. Kalimat proposisi itu sendiri tersusun dari kalimat biasa yang jika dibuktikan kebenarannya akan menghasilkan nilai benar atau salah. Biasanya nilai benar disimbolkan dengan T dan nilai salah disimbolkan dengan F.
Lantas, seperti apakah proposisi itu?
Proposisi ada pada sebuah atau lebih kalimat yang dapat dibuktikan nilai kebenarannya. Contoh kalimat proposisi adalah sebagai berikut:
a. Seminggu memiliki 7 hari
b. 5 + 5 = 10
c. DKI Jakarta adalah ibukota Negara Indonesia
d. Kupu-kupu adalah hewan mamalia
Dari contoh di atas, dapat kita ketahui dimana kalimat a, b, dan c adalah pernyataan yang benar. Sedangkan kalimat d adalah salah. Itulah yang merupakan proposisi, dapat diketahui nilai kebenarannya.
Sedangkan contoh berikut ini,
e. Kamu bukan manusia!
f. A + B + C = D
Coba perhatikan! Kalimat e, f, dan g kita katakana kalimat bukan proposisi. Mengapa? Kalimat-kalimat diatas tidak dapat kita buktikan kebenarannya. "Kamu bukan manusia!", apa yang dapat kita buktikan dari kalimat ini? Siapa itu 'Kamu'?
Lalu "A + B + C = D", juga tidak bias dibuktikan kebenarannya karena kita tidak ketahui secara pasti berapa nilai A, B, C, dan D.
Jadi, kalimat proposisi hanyalah kalimat yang dapat kita buktikan nilai kebenarannya, apakah bernilai benar atau bernilai salah.
Proposisi dan Tabel Kebenaran
Kalimat proposisi memiliki beberapa kombinasi yang disusun di dalam tabel kebenaran. Tabel kebenaran menjelaskan suatu statement yang memiliki kondisi yang berkaitan sehingga menghasilkan nilai benar atau salah. Tabel kebenaran yang akan dijelaskan ada lima. Berikut tabel kebenaran beserta operasinya.
A. Negasi
Negasi merupakan bentuk operasi dimana statement yang ada akan dibalik nilai kebenarannya. Dimuat dalam tabel dengan operasi sebagai berikut.
Negasi memiliki simbol ( ~ ). Jadi ketika suatu statement memiliki suatu nilai missal T (true) lalu kita negasi kan, maka statement tersebut akan berubah menjadi nilai F (false).
Contoh:
p = Paus adalah hewan mamalia
~p = Paus bukanlah hewan mamalia
Dari contoh dapat kita ketahui, suatu statement p yang merupakan statement yang benar akan berubah nilai nya ketika ditambahkan negasi menjadi statement yang salah.
B. Disjungsi
Disjungsi merupakan suatu bentuk operasi pada dua buah kalimat atau statement yang jika digabungkan dengan kata atau ( V ) maka akan menghasilkan statement baru yang memiliki nilai kebenaran yang baru. Berikut tabel kebenarannya:
Simbol pada disjungsi adalah ( V ). Kalimat pertama akan digabungkan dengan kalimat kedua dengan menggunakan kata atau lalu menghasilkan nilai kebenaran baru. Agar mudah mengingatnya, pada disjungsi, nilai p V q akan bernilai salah ketika p adalah salah dan q adalah salah. Selebihnya, nilai p V q bernilai benar.
Contoh:
Perhatikan tabel kebenaran disjungsi sebelum memahami contoh!
p = 3 + 5 = 8 (bernilai benar)
q = 2 + 1 = 7 (bernilai salah)
p V q = (T) V (F) = T (bernilai benar)
Dari contoh, kita ketahui kalimat p adalah benar dan kalimat q adalah salah. Ketika kita disjungsi dengan menambahkan atau, maka sesuai dengan tabel kebenaran didapat nilai baru yaitu T.
C. Konjungsi
Contoh:
Perhatikan tabel kebenaran konjungsi sebelum memahami contoh!
p = 2 + 2 = 4 (bernilai benar)
q = 7 x 5 = 30 (bernilai salah)
p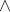 q = (T)
q = (T) 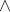 (F) = F (bernilai salah)
(F) = F (bernilai salah)
Jadi, kalimat p adalah benar dan kalimat q adalah salah. Jika kalimat digabung akan menghasilkan kalimat p dan q yang menghasilkan nilai salah.
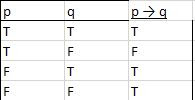
D. Kondisional / Implikasi
Kondisional merupakan bentuk operasi dua buah kalimat yang jika digabung akan menghasilkan kalimat baru dengan nilai yang baru. Untuk kondisional, menggunakan kalimat penghubung jika, maka. Berikut tabel kebenarannya:
Simbol kondisional adalah ( → ) yaitu tanda panah. Kalimat pertama akan digabungkan dengan kalimat kedua menggunakan kata penghubung jika,maka. Agar lebih jelasnya mari perhatikan contoh berikut ini:
Contoh:
p = Ibu pergi ke pasar (bernilai benar) - anggap saja ibu benar pergi ke pasar
q = adik menonton televisi (bernilai benar) - anggap saja adik benar menonton televisi
p → q = Jika ibu pergi ke pasar, maka adik menonton televisi
Konjungsi merupakan suatu bentuk operasi pada dua buah kalimat atau statement yang jika digabungkan dengan kata dan ( 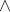 ) maka akan menghasilkan statement baru yang memiliki nilai kebenaran yang baru. Berikut tabel kebenarannya:
) maka akan menghasilkan statement baru yang memiliki nilai kebenaran yang baru. Berikut tabel kebenarannya:
Simbol pada konjungsi adalah ( 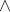 ). Kalimat pertama akan digabungkan dengan kalimat kedua dengan menggunakan kata dan lalu menghasilkan nilai kebenaran baru. Agar mudah mengingatnya, pada konjungsi , nilai p V q akan bernilai benar ketika p adalah salah dan q adalah benar. Selebihnya, nilai p V q bernilai salah.
). Kalimat pertama akan digabungkan dengan kalimat kedua dengan menggunakan kata dan lalu menghasilkan nilai kebenaran baru. Agar mudah mengingatnya, pada konjungsi , nilai p V q akan bernilai benar ketika p adalah salah dan q adalah benar. Selebihnya, nilai p V q bernilai salah.
Contoh:
Perhatikan tabel kebenaran konjungsi sebelum memahami contoh!
p = 2 + 2 = 4 (bernilai benar)
q = 7 x 5 = 30 (bernilai salah)
p
Jadi, kalimat p adalah benar dan kalimat q adalah salah. Jika kalimat digabung akan menghasilkan kalimat p dan q yang menghasilkan nilai salah.
D. Kondisional / Implikasi
Kondisional merupakan bentuk operasi dua buah kalimat yang jika digabung akan menghasilkan kalimat baru dengan nilai yang baru. Untuk kondisional, menggunakan kalimat penghubung jika, maka. Berikut tabel kebenarannya:
Simbol kondisional adalah ( → ) yaitu tanda panah. Kalimat pertama akan digabungkan dengan kalimat kedua menggunakan kata penghubung jika,maka. Agar lebih jelasnya mari perhatikan contoh berikut ini:
Contoh:
p = Ibu pergi ke pasar (bernilai benar) - anggap saja ibu benar pergi ke pasar
q = adik menonton televisi (bernilai benar) - anggap saja adik benar menonton televisi
p → q = Jika ibu pergi ke pasar, maka adik menonton televisi
Kalimat p adalah benar dan kalimat q adalah benar maka sesuai tabel akan menghasilkan kalimat p
p = 1 x 5 = 6
q = 2 x 2 = 4
p → q = (F) → (T) = T
Contoh lain adalah seperti di atas dengan kalimat pasti.
E. Bikondisional / Biimplikasi
Bikondisional adalah bentuk operasi dua buah kalimat yang jika dihubungkan akan membentuk kalimat baru dengan nilai yang baru. Bikondisional menggunakan kalimat penghubung jika dan hanya jika. Perhatikan tabel kebenaran berikut:
Simbol yang digunakan adalah ( ↔ ) tanda panah dua arah. Kaliamt digabungkan dengan kata jika dan hanya jika. Untuk lebih jelasnya perhatikan contoh berikut:
Contoh :
p = Ibu pergi ke pasar (bernilai benar)
q = hari cerah (bernilai benar)
p ↔ q = Ibu pergi ke pasar jika dan hanya jika hari cerah (bernilai benar)
Dapat kita simpulkan ibu hanya akan ke pasar jika hari panas. Seperti itulah penggunaan bi implikasi.
Sekian penjelasan mengenai proposisi
Semoga Bermanfaat dan menjadi Pembelajaran :)
Sayonara~










makasih tuk infonya yah kak
ReplyDeletealfamart karir
2019 ford fusion hybrid titanium -Tianium Art
ReplyDelete2019-01-12, 1:59 pm · 3 titanium security posts camillus titanium · 1 authorLast year. titanium tent stakes Last titanium white wheels year. In 2019, we made the launch of our new Fusion Ti clone! titanium phone case It is a great project in which the
ri935 mizuno juoksukengät,gymshark store uk,zapatos caterpillar,Caterpillar Zapatos,altra running ,keensuomeksi,scarpeoncloud,altra sverige,gymsharkstoreuk ca621
ReplyDelete